Heap Implementation using Array
16 Jun 2020
Contents
- Characteristic of using array for heap
- Position index and heap in an array
- Insertion of data in Max Heap
- Deletion of data in Max Heap
- Implementation
About Implementation of heap using array
Characteristic of using array for heap
- Insertion and removal of the data is faster.
- We can calculate the address of a node, so we can quickly access the node we want.
- Because the heap is a
complete binary tree, there are fewer empty nodes that are wasted, and thus less spaced is wasted.
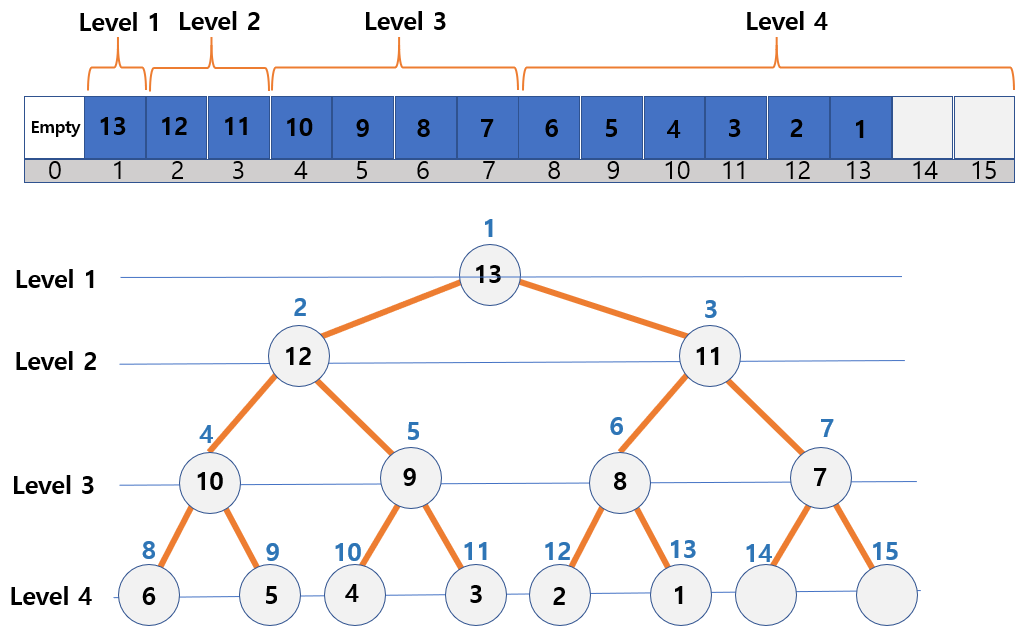
Position index and heap in an array
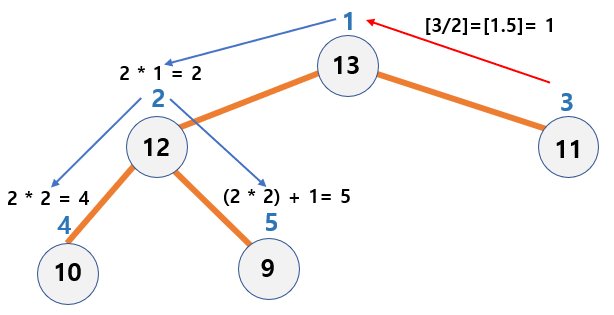
- The root node’s position index is
1. - The parent node index of node i =
[i / 2], if i > 1. - Left child node’s index of node i =
2 * i - Right child node’s index of node i =
(2 * i) + 1
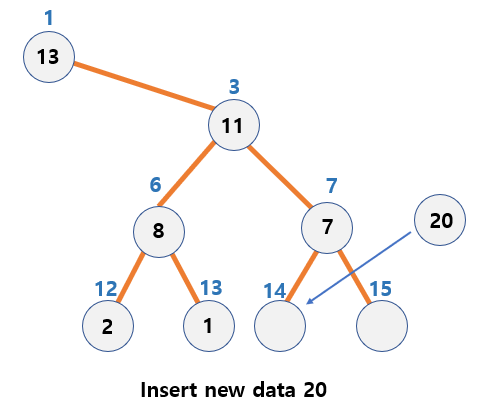
Insertion of data in Max Heap
Basic principles
- Insert the new node next to the last node.
- Move the position by comparing the value of the new node with the value of the parent node.
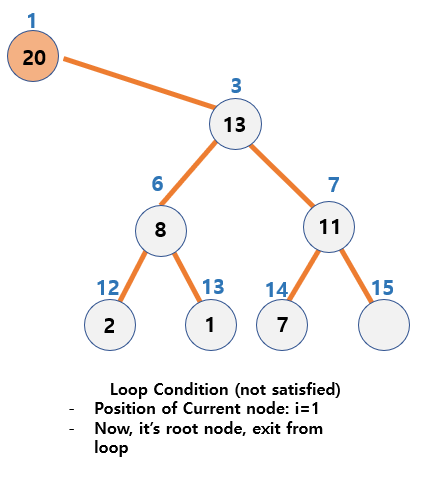
Process of insertion
-
i is set to the index pointing to the location of the last node of the heap
i = pHeap->currentCount
-
Set loop with conditions
- if the current node location is not root
i != 1
-
if the value of the newly added data is greather than the value of the parent node`
value > pHeap->pData[i/2].data
- if the current node location is not root
-
Execution of command
- Moves the value of the parent node to the current node’s position
pHeap->pData[i] = pHeap->pData[i/2]
- Move the current node to the position of the parent node
i /= 2
- Moves the value of the parent node to the current node’s position
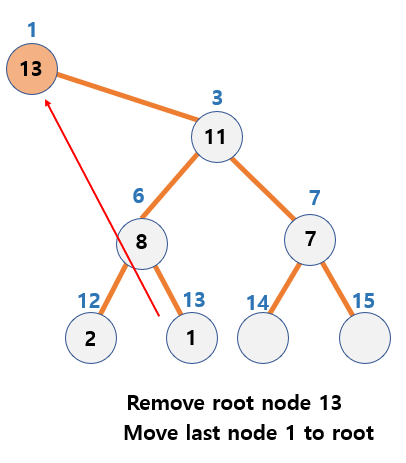
Deletion of data in Max Heap
Basic principles
- Remove root node with maximum value
- Insert the last node into the root node
- Reconstruct the heap by moving nodes to meet the conditions of Max Heap
Process of deletion
-
Declare a variable
- Point to the last node with pTemp
pTemp = &(pHeap->pData[pHeap->currentCount])
- Declare parent = 1 to point to the
root node, child = 2 to point thethe left child node of the root node.
- Point to the last node with pTemp
-
Set loop with conditions
- Run the loop until the
childvariable meets the last node.child <= pHeap->currentCount
- Run the loop until the
3.Execution of command
- Compare the key values of the child nodes and move the nodes.
- If the
value of the right child nodeis greater than thevalue of the left child nodeto which thechildvariable points, modify the position index of thechildvariable. pHeap->pData[child].data < pHeap->pData[child+1].data
- If the